De l’ACP à la Régression sous Google Colab

Charger les données

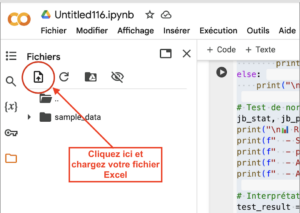
Trouvez le chemin d’accès aux données

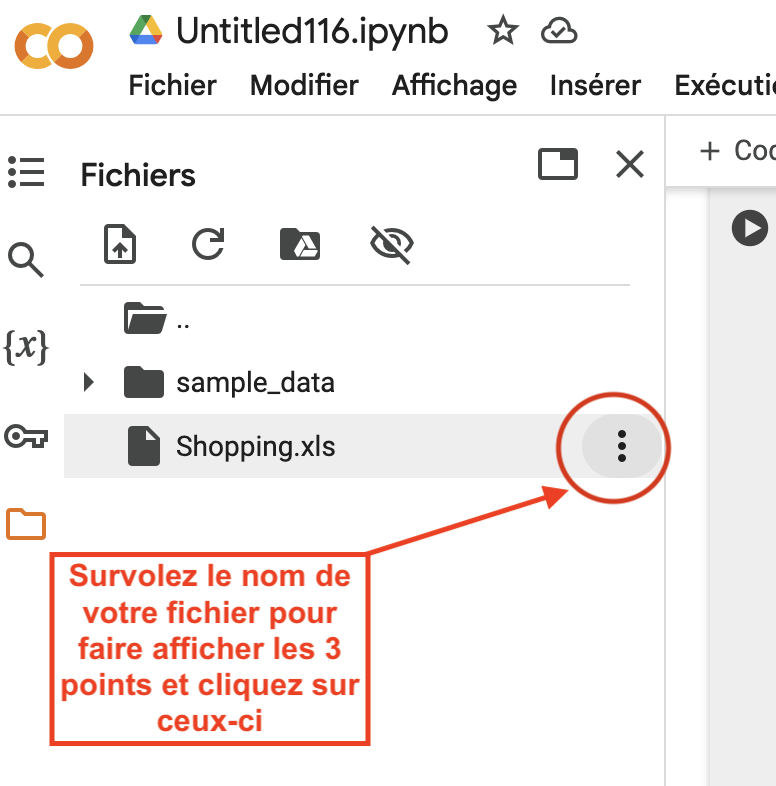
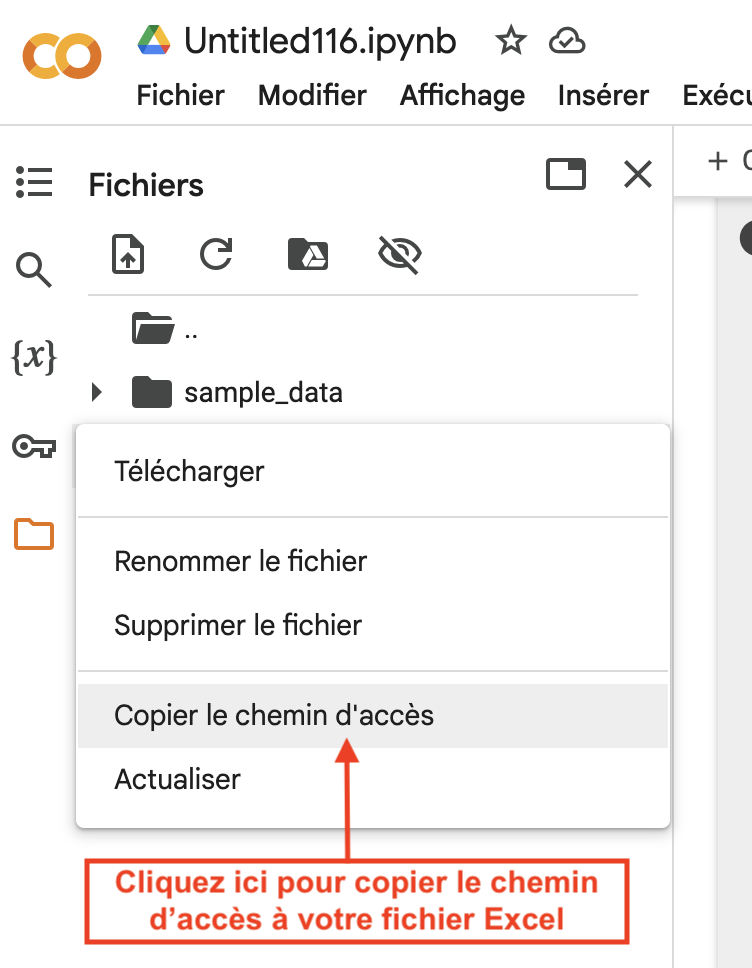
Copiez le chemin d’accès aux données

Chargez les bibliothèques nécessaires

Copiez le code ci-dessous et collez-le sous Google Colab :

import pandas as pd

# Demander à l'utilisateur d'entrer le chemin du fichier
file_path = input("Veuillez coller le chemin complet du fichier XLS : ")

# Charger le fichier XLS dans un DataFrame
data_original = pd.read_excel(file_path)

# Afficher le contenu du DataFrame
data_original

Installer les bibliothèques nécessaires

Copiez le code ci-dessous et collez-le sous Google Colab :

!pip install factor_analyzer
!pip install --upgrade scikit-learn
!pip install --upgrade --no-deps scikit-learn
!pip install --upgrade imbalanced-learn xgboost

Procéder à l’Analyse en Composantes Principales sans rotation

Copiez le code ci-dessous et collez-le sous Google Colab :

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from factor_analyzer import FactorAnalyzer
from factor_analyzer.factor_analyzer import calculate_kmo, calculate_bartlett_sphericity
from ipywidgets import interactive
import ipywidgets as widgets

# Fonction pour calculer l'alpha de Cronbach
def cronbach_alpha(df):
  if len(df.columns) > 1:
    k = df.shape[1]
    variances = df.var(axis=0, ddof=1)
    total_variance = df.sum(axis=1).var(ddof=1)
    return (k / (k - 1)) * (1 - (variances.sum() / total_variance))
  
  else:
    print("⚠️ Pas assez de variables pour calculer l'alpha sans item.")

# Chargement des données (supposées déjà chargées dans data_original)
def select_columns(data):
    print("\nColonnes disponibles :", list(data.columns))
    selected_columns = input("Entrez les noms des colonnes pour l'ACP (séparées par une virgule) : ").strip().split(',')
    selected_columns = [col.strip() for col in selected_columns]
    if not all(col in data.columns for col in selected_columns):
        print("Erreur : certaines colonnes n'existent pas. Réessayez.")
        return select_columns(data)
    return selected_columns

# Étape 1 : Sélection des colonnes pour l'ACP
selected_columns = select_columns(data_original)
df = data_original[selected_columns]

# Étape 2 : Normalisation des données
scaler = StandardScaler()
data_scaled = scaler.fit_transform(df)

# Étape 3 : Test KMO et Bartlett
kmo_all, kmo_model = calculate_kmo(df)
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(f"\nKMO global : {kmo_model:.3f}")
print(f"Test de Bartlett : Chi² = {chi_square_value:.3f}, p = {p_value:.3f}")

# Étape 4 : Communalités
# Affichage des communalités
fa_temp = FactorAnalyzer(rotation=None, method='principal', is_corr_matrix=False)
fa_temp.fit(data_scaled)
eigenvalues, _ = fa_temp.get_eigenvalues()
n_factors = sum(eigenvalues > 1)
print(f"Nombre de composantes retenues (valeurs propres > 1) : {n_factors}")
fa_temp = FactorAnalyzer(rotation=None, method='principal', n_factors=n_factors,is_corr_matrix=False)
fa_temp.fit(data_scaled)
communalities = pd.DataFrame({
    'Variable': df.columns,
    'Initial': [1.000] * len(df.columns),  # Les valeurs initiales sont toujours 1
    'Communalité': fa_temp.get_communalities()
}).round(3)
print("\nCommunalités des variables:")
print(communalities)

# Étape 5 : Détermination du nombre de facteurs
eigenvalues, _ = fa_temp.get_eigenvalues()
n_factors = sum(eigenvalues > 1)
print(f"Nombre de composantes retenues (valeurs propres > 1) : {n_factors}")

# Tableau des variances expliquées
explained_variance_ratio = eigenvalues / np.sum(eigenvalues)
cumulative_variance = np.cumsum(explained_variance_ratio)
variance_table = pd.DataFrame({
    'Composante': [f"Composante {i+1}" for i in range(len(eigenvalues))],
    'Valeurs propres': eigenvalues,
    'Variance expliquée (%)': explained_variance_ratio * 100,
    'Variance expliquée cumulée (%)': cumulative_variance * 100
}).round(3)
display(variance_table)

# Graphique Scree Plot
plt.figure(figsize=(8, 6))
plt.plot(range(1, len(eigenvalues) + 1), eigenvalues, marker='o')
plt.title("Graphique des valeurs propres (Scree Plot)")
plt.xlabel("Composantes")
plt.ylabel("Valeurs propres")
plt.grid(True)
plt.show()

# Étape 6 : Choix du nombre de facteurs par l'utilisateur

# Demander à l'utilisateur le nombre de composantes à retenir au moment de la sauvegarde
n_factors = int(input("Entrez le nombre de composantes à retenir pour les scores factoriels : "))

# Étape 7 : Analyse factorielle avec le nombre de facteurs sélectionné
fa = FactorAnalyzer(rotation=None, method='principal', n_factors=n_factors)
fa.fit(data_scaled)

# Matrice des charges factorielles
loadings = fa.loadings_
components_matrix = pd.DataFrame(loadings, index=df.columns).round(3)
display(components_matrix)

# Étape 8 : Cercle des corrélations
if n_factors > 1:
    fig, ax = plt.subplots(figsize=(6, 6))
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.axhline(0, color='black', linestyle='-', linewidth=0.8)
    ax.axvline(0, color='black', linestyle='-', linewidth=0.8)
    ax.grid(True, linestyle='--', linewidth=0.5, alpha=0.7)
    for i in range(loadings.shape[0]):
        ax.scatter(loadings[i, 0], loadings[i, 1], color='b', alpha=0.5, s=50)
        ax.text(loadings[i, 0], loadings[i, 1], df.columns[i], color='r', fontsize=8, ha='center')
    ax.set_title("Cercle des corrélations", fontsize=10)
    ax.set_xlabel("Composante 1")
    ax.set_ylabel("Composante 2")
    plt.show()

# Demander à l'utilisateur s'il souhaite une rotation
rotation_choice = input("Souhaitez-vous procéder à une rotation des variables ? (oui/non) : ").strip().lower()

if rotation_choice == "non":
    fa = FactorAnalyzer(n_factors=n_factors, rotation=None, method='principal')
    fa.fit(data_scaled)
    factor_scores = fa.transform(data_scaled)
    # Demander à l'utilisateur le nom des composantes
    component_names = []
    for i in range(n_factors):
      name = input(f"Entrez le nom pour la composante {i+1} : ")
      component_names.append(name)
    components_matrix.columns = component_names


    factor_scores_df = pd.DataFrame(factor_scores, columns=component_names)

    # Affichage des scores factoriels
    display(factor_scores_df)

    
    # Calcul de l'alpha de cronbach
    global_alpha = cronbach_alpha(df)
    print(f"Alpha de Cronbach global : {global_alpha:.3f}")
    
    alpha_sans_item = {col: cronbach_alpha(df.drop(columns=[col])) for col in selected_columns}
    df_alpha = pd.DataFrame.from_dict(alpha_sans_item, orient='index', columns=['Alpha sans item']).round(3)
    display(df_alpha)


############# ROTATION ##################@@



else:
    rotation_types = ["varimax", "promax", "oblimin", "quartimax"]
    print("Types de rotation disponibles :", rotation_types)
    rotation_type = input("Veuillez entrer le type de rotation souhaité : ").strip().lower()
    
    if rotation_type not in rotation_types:
        print("Type de rotation non valide. Par défaut, 'varimax' sera utilisé.")
        rotation_type = "varimax"
    
    fa = FactorAnalyzer(n_factors=n_factors, rotation=rotation_type, method='principal')
    fa.fit(data_scaled)
    loadings = fa.loadings_
    components_matrix = pd.DataFrame(loadings, index=df.columns).round(3)


# Affichage des scores factoriels
#    display(factor_scores_df)

# Étape 8 : Cercle des corrélations
    if n_factors > 1:
        fig, ax = plt.subplots(figsize=(6, 6))
        ax.set_xlim(-1, 1)
        ax.set_ylim(-1, 1)
        ax.axhline(0, color='black', linestyle='-', linewidth=0.8)
        ax.axvline(0, color='black', linestyle='-', linewidth=0.8)
        ax.grid(True, linestyle='--', linewidth=0.5, alpha=0.7)
        for i in range(loadings.shape[0]):
            ax.scatter(loadings[i, 0], loadings[i, 1], color='b', alpha=0.5, s=50)
            ax.text(loadings[i, 0], loadings[i, 1], df.columns[i], color='r', fontsize=8, ha='center')
        ax.set_title("Cercle des corrélations", fontsize=10)
        ax.set_xlabel("Composante 1")
        ax.set_ylabel("Composante 2")
        plt.show()

# Demander à l'utilisateur le nom des composantes
    component_names = []
    for i in range(n_factors):
      name = input(f"Entrez le nom pour la composante {i+1} : ")
      component_names.append(name)
    components_matrix.columns = component_names
    factor_scores = fa.transform(data_scaled)
    factor_scores_df = pd.DataFrame(factor_scores, columns=component_names)

    # Affichage des scores factoriels
    display(factor_scores_df)
    global_alpha = cronbach_alpha(df)
    print(f"Alpha de Cronbach global : {global_alpha:.3f}")
    
    alpha_sans_item = {col: cronbach_alpha(df.drop(columns=[col])) for col in selected_columns}
    df_alpha = pd.DataFrame.from_dict(alpha_sans_item, orient='index', columns=['Alpha sans item']).round(3)
    display(df_alpha)

# Demander à l'utilisateur s'il souhaite enregistrer les résultats
def save_results():
    global data_original
    data_original = pd.concat([data_original, factor_scores_df], axis=1)
    output_file = "Analyse_Factorielle_Resultats.xlsx"
    with pd.ExcelWriter(output_file) as writer:
        factor_scores_df.to_excel(writer, sheet_name="Scores_Factoriels", index=False)
        df_alpha.to_excel(writer, sheet_name="Alpha_Cronbach", index=True)
    print(f"\nLes résultats ont été sauvegardés dans {output_file}.")

save_btn = widgets.Button(description="Enregistrer les résultats")
save_btn.on_click(lambda b: save_results())
display(save_btn)

Procéder à la régression

Copiez le code ci-dessous et collez-le sous Google Colab :

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor

# Sélectionner les variables explicatives (X) et la variable dépendante (y)
y_var = input("Entrez le nom de la variable dépendante : ").strip()
X_vars = input("Entrez les noms des variables explicatives (séparés par une virgule) : ").strip().split(",")

# Vérification des variables
if y_var not in data_original.columns or any(var not in data_original.columns for var in X_vars):
    raise ValueError("Erreur : Assurez-vous que toutes les variables existent dans le DataFrame.")

# Définir X et y
X = data_original[X_vars]  # Suppression de l'ajout de la constante
y = data_original[y_var]

# Vérifier si X contient au moins une variable
if X.shape[1] == 0:
    raise ValueError("Erreur : Aucune variable explicative valide sélectionnée.")

# Ajustement du modèle OLS
model = sm.OLS(y, X).fit()
print(model.summary())

# Vérification de la normalité des résidus avec un QQ-plot
residuals = model.resid
fig, ax = plt.subplots(figsize=(6, 6))
sm.qqplot(residuals, line="s", ax=ax)
ax.set_title("QQ-Plot des résidus")
plt.show()

# Vérification de l'hétéroscédasticité avec un scatter plot
plt.figure(figsize=(8, 5))
sns.scatterplot(x=model.fittedvalues, y=residuals)
plt.axhline(0, linestyle="dashed", color="red")
plt.xlabel("Valeurs ajustées")
plt.ylabel("Résidus")
plt.title("Graphique des résidus")
plt.show()

# Calcul du VIF pour détecter la multicolinéarité
if X.shape[1] > 1:  # Vérifier que le VIF peut être calculé
    vif_data = pd.DataFrame({
        "Variable": X.columns,
        "VIF": [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
    })
    print("\n📊 Facteur d'inflation de la variance (VIF) :")
    display(vif_data)

    # Interprétation du VIF
    high_vif = vif_data[vif_data["VIF"] > 10]
    if not high_vif.empty:
        print("\n⚠️ Attention : Certaines variables présentent une forte multicolinéarité (VIF > 10). Cela peut affecter la fiabilité des coefficients estimés.")
        print(high_vif)
    else:
        print("✅ Aucune multicolinéarité préoccupante détectée (VIF < 10).")
else:
    print("\n⚠️ Pas assez de variables pour calculer le VIF.")

# Test de normalité des résidus (Jarque-Bera)
jb_stat, jb_pvalue, skew, kurtosis = sm.stats.jarque_bera(residuals)
print("\n📊 Résultats du Test de normalité de Jarque-Bera :")
print(f"  - Statistique JB : {jb_stat:.3f}")
print(f"  - p-value : {jb_pvalue:.5f}")
print(f"  - Asymétrie (Skewness) : {skew:.3f}")
print(f"  - Aplatissement (Kurtosis) : {kurtosis:.3f}")

# Interprétation automatique
test_result = "✅ Les résidus suivent une loi normale (p > 0.05)." if jb_pvalue > 0.05 else "❌ Les résidus ne suivent PAS une loi normale (p ≤ 0.05)."
print(f"\n{test_result}")

if jb_pvalue <= 0.05:
    if abs(skew) > 1:
        print("🔍 Problème détecté : **Asymétrie élevée** (skewness).")
        print("✅ Solution : Essayez une transformation logarithmique ou une normalisation.")
    if kurtosis < 2 or kurtosis > 4:
        print("🔍 Problème détecté : **Aplatissement anormal (kurtosis).**")
        print("✅ Solution : Vérifiez s'il y a des valeurs aberrantes (outliers).")

    print("\n📌 Recommandations supplémentaires :")
    print("  - Vérifiez la présence de valeurs aberrantes avec un boxplot.")
    print("  - Testez une transformation (log, carré, racine) sur la variable dépendante.")
    print("  - Ajoutez éventuellement d'autres variables explicatives.")

# Conclusion générale
print("\n📌 **Conclusion** :")
print("  - L'ajustement du modèle est évalué avec le R² et le R² ajusté.")
print("  - Un R² élevé (>0.7) indique une bonne capacité explicative du modèle, tandis qu'un R² faible suggère un ajustement limité.")
print("  - Les coefficients et leurs p-values indiquent la significativité des variables explicatives : une p-value < 0.05 signifie que la variable a un impact significatif.")
print("  - Le VIF aide à détecter la multicolinéarité, qui peut biaiser les estimations.")
print("  - Le test de Jarque-Bera vérifie la normalité des résidus, influençant la validité des tests de significativité.")