Méthodologie du Travail de Recherche

Déroulement de l’Étude Expérimentale

1. Le terrain d’investigation

L’étude expérimentale repose sur une exploration du terrain afin d’identifier le contexte et les acteurs impliqués. Il est crucial de définir précisément le cadre de l’étude, qu’il s’agisse d’une enquête auprès de consommateurs, d’une analyse de comportements en entreprise ou d’une étude de cas spécifique. La délimitation du terrain permet d’assurer une cohérence entre la problématique et les données collectées.

2. Le choix des répondants

La sélection des répondants est une étape déterminante dans la validité des résultats. Il est nécessaire d’adopter un échantillonnage représentatif, aligné avec les objectifs de l’étude. La méthode d’échantillonnage peut être probabiliste (échantillonnage aléatoire simple, stratifié) ou non probabiliste (échantillonnage par convenance, boule de neige). Les critères de sélection des participants doivent être définis en fonction des caractéristiques pertinentes à analyser, telles que l’âge, le secteur d’activité ou les habitudes de consommation.

3. La méthode de collecte des données

La collecte des données peut être réalisée par différentes techniques selon l’approche retenue. Dans le cadre d’une étude quantitative, le recours aux questionnaires en ligne ou en face-à-face est fréquent. Pour une approche qualitative, les entretiens semi-directifs, les focus groups ou l’observation participante peuvent être privilégiés. La méthode choisie doit garantir l’objectivité et la fiabilité des données collectées.

4. La construction du questionnaire final

La conception du questionnaire repose sur une adaptation des échelles de mesure issues de la littérature scientifique. Chaque concept du modèle est évalué à l’aide de plusieurs items afin d’assurer une mesure valide et fiable. Les questions sont généralement formulées selon une échelle de Likert (ex. : de 1 = Pas du tout d’accord à 7 = Tout à fait d’accord).

L’objectif du questionnaire est de permettre une analyse statistique rigoureuse en limitant les biais de réponse. Une pré-test du questionnaire peut être réalisé auprès d’un échantillon réduit afin d’identifier d’éventuelles ambiguïtés ou incohérences.

5. Les caractéristiques de l’échantillon étudié

La description de l’échantillon comprend plusieurs éléments :

• Le nombre de participants et le taux de réponse obtenu.
• Les caractéristiques sociodémographiques des répondants (âge, sexe, catégorie socioprofessionnelle, etc.).
• Les comportements spécifiques des individus interrogés en lien avec l’objet de l’étude.

L’analyse descriptive de ces données permet d’assurer que l’échantillon est représentatif et adapté aux objectifs de recherche.

---

La Procédure de Test, le Choix et la Validation des Instruments de Mesure Retenus

1. La procédure de test des instruments de mesure

Cette section est consacrée à la procédure de test des instruments de mesure détaillera les méthodes employées pour évaluer la fiabilité et la validité des échelles utilisées dans l’étude. Cette validation repose sur des analyses statistiques rigoureuses, en particulier l’Analyse en Composantes Principales (ACP) et l’alpha de Cronbach.

Ces deux méthodes doivent être expliquées en soulignant comment elles sont utilisées pour garantir que les instruments de mesure sont adaptés et valides avant d’analyser les résultats de l’étude.

2. Le choix et la validation des instruments de mesure retenus

2.1. Les critères de choix des différents instruments de mesure

Cette section vise à justifier la sélection des échelles de mesure utilisées dans l’étude. Le choix des instruments de mesure est une étape cruciale, car il détermine la pertinence et la fiabilité des données collectées. Le choix des échelles repose sur des critères tels que leur validité théorique, leur utilisation dans des études antérieures et leur capacité à mesurer fidèlement le phénomène étudié.

L’objectif est de s’assurer que les échelles retenues permettent de mesurer précisément le phénomène étudié en se basant sur trois critères essentiels :

• La Validité Théorique : Les échelles doivent être ancrées dans la littérature scientifique et correspondre aux concepts théoriques définis dans le modèle de recherche. Une échelle est considérée comme valide si elle a été développée à partir de théories reconnues et validées dans des études académiques.
• L’Utilisation dans des Études Antérieures : Il est essentiel de privilégier des échelles ayant déjà été employées et testées dans des recherches similaires. Cela permet de garantir leur fiabilité et leur adéquation au contexte étudié, tout en assurant une comparabilité des résultats avec d’autres travaux.
• La Capacité à Mesurer Fidèlement le Phénomène : Une échelle pertinente doit couvrir l’ensemble des dimensions du concept étudié et être suffisamment précise pour distinguer des variations significatives dans les réponses des participants. Elle doit également présenter des qualités psychométriques solides, comme une cohérence interne élevée (alpha de Cronbach) et une bonne validité factorielle.

Cette section permet donc d’expliquer les choix méthodologiques justifiant l’adoption des échelles de mesure et de démontrer leur pertinence dans le cadre de l’étude menée.

2.2. Les échelles de mesure retenues

Cette section s’intéresse à l’évaluation des échelles de mesure utilisées dans l’étude afin d’assurer leur validité et leur fiabilité. En effet, une fois les données collectées, il est essentiel d’évaluer la validité et la fiabilité des échelles utilisées.
Les échelles de mesure sélectionnées doivent être opérationnalisées et adaptées au contexte de l’étude. L’explication détaillée de leur origine et de leur validité théorique permet de garantir la solidité des analyses à venir. Après la collecte des données, plusieurs analyses statistiques sont effectuées pour garantir que les items mesurent bien le concept théorique auquel ils sont associés.
Un tableau synthétique viendra présenter les résultats obtenus pour chacun des outils de mesure utilisés comme vous pouvez le voir içi :

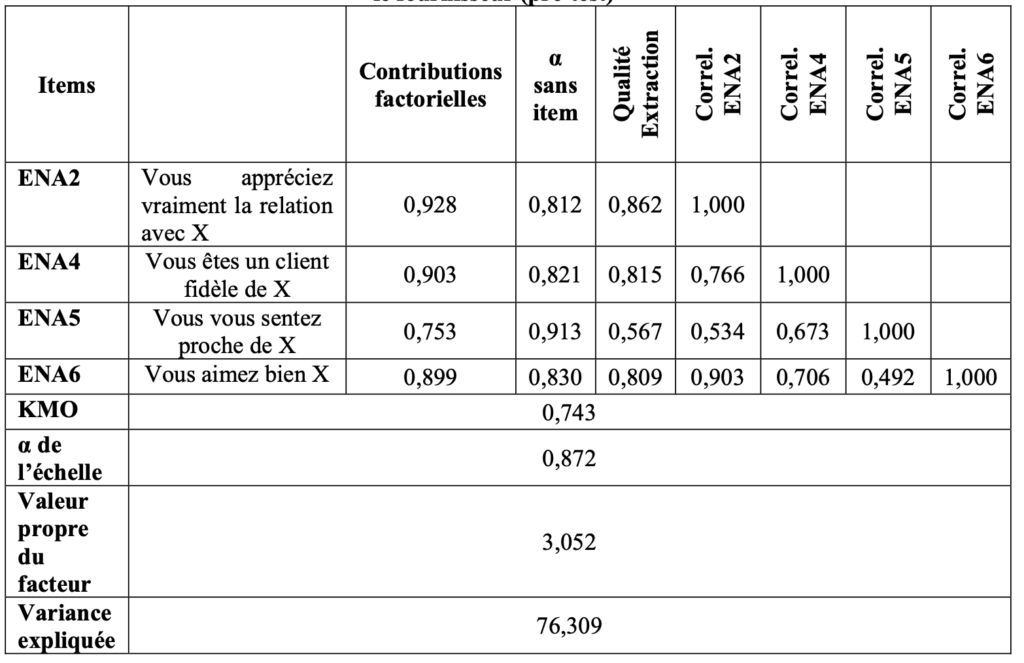
La première étape consiste en une purification des échelles, qui permet d’éliminer les items non pertinents ou redondants grâce à des indicateurs comme la corrélation item-total et l’alpha de Cronbach.

Ensuite, une analyse factorielle exploratoire (AFE) est réalisée pour identifier la structure sous-jacente des échelles et regrouper les items en facteurs cohérents. Cette analyse repose sur plusieurs tests, notamment :

• Le test KMO et le test de Bartlett, qui vérifient l’adéquation des données à une analyse factorielle.
• L’analyse en composantes principales (ACP) et la rotation factorielle (ex. : Varimax), qui facilitent l’interprétation des résultats.
• L’examen de la variance totale expliquée, qui mesure la part du phénomène étudié capturée par les facteurs extraits.

La robustesse des mesures est ensuite évaluée à travers les contributions factorielles des items et leur qualité de représentation. Un item est considéré comme fiable si sa charge factorielle est élevée et si l’alpha de Cronbach dépasse 0,7, garantissant ainsi une bonne cohérence interne.

L’ensemble de ces analyses permet de valider les instruments de mesure retenus et d’assurer leur pertinence pour tester les hypothèses du modèle de recherche.

---

Les Choix Méthodologiques pour le Test des Hypothèses

Les hypothèses du modèle sont testées à l’aide de méthodes statistiques adaptées. Parmi les techniques les plus utilisées, on retrouve :

1. Les régressions linéaires, qui permettent d’analyser l’influence d’une variable indépendante sur une variable dépendante.
2. Les analyses de variance (ANOVA), qui comparent les différences entre plusieurs groupes de répondants.
3. Les modèles d’équations structurelles, qui évaluent l’ensemble des relations d’un modèle théorique en une seule analyse globale.

Ces analyses permettent de déterminer si les hypothèses formulées dans le cadre du travail de recherche sont confirmées ou non.

---

L’approche méthodologique adoptée garantit la rigueur scientifique de l’étude en s’appuyant sur des analyses fiables et validées. L’ensemble du processus, depuis la construction du questionnaire jusqu’aux tests statistiques, permet d’assurer des résultats robustes et interprétables. Ce travail ne vise pas à valider définitivement des hypothèses, mais à les mettre à l’épreuve du réel, contribuant ainsi à l’enrichissement des connaissances dans le domaine étudié.

---

CODE PYTHON ACP

Vous devez réaliser une ACP pour chaque concept étudié (Normes Subjectives, Risques Perçus, etc., y compris l’intention de payer en BTC) en utilisant le code Python ci-après :

• installation des bibliothèques Python,
• lire les données,
• réaliser l’ACP.

Cette ACP permettra de réduire la dimensionnalité des données et d’extraire un score factoriel unique pour chaque individu sur chaque concept.

L’alpha de Cronbach que vous avez calculé représente un indicateur de fiabilité de votre échelle de mesure et montre la cohérence interne des échelles.

• Attention :
  • Une fois les bibliothèques installées et les données lues, n’utiliser que le code réaliser l’ACP. Dans le cas contraire, les scores factoriels enregistrés seront effacés
  • Le nom de la composante extraite ne doit pas comprendre d’apostrophe, d’espace ou de caractère avec accent. Il vous faut trouver un codage unique et simple (exemple : nom du concept = normes subjective, nom de la composante = NornesSubjectives)
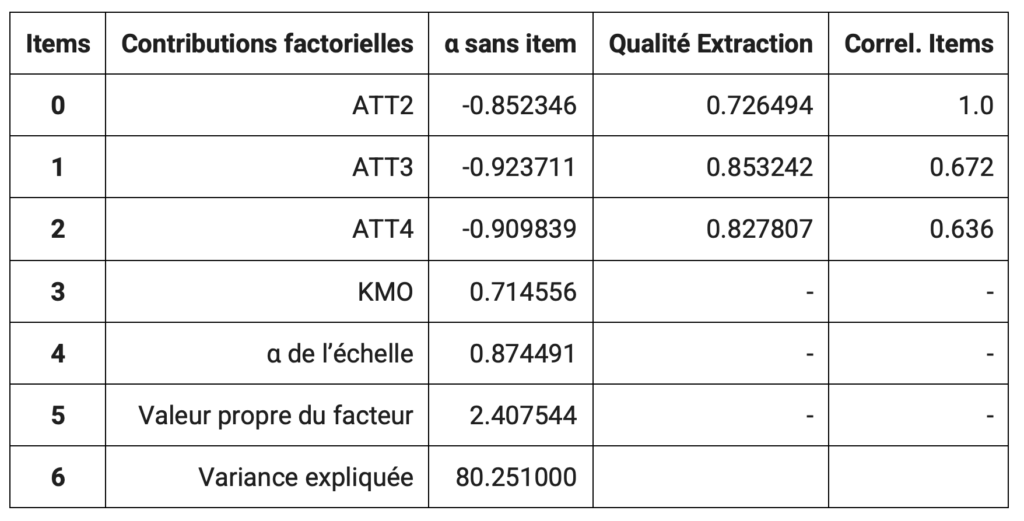
  • Pensez à copier/coller le tableau de synthèse avec de cliquer sur “enregistrer les résultats” :

Voici ci-après, le code Pyhton à utiliser pour vérifier la structure factorielle de vos mesures et obtenir les résultats à intégrer dans la régression multiple :

Charger le fichier de données

Copiez le code ci-dessous et collez-le sous Google Colab :

import pandas as pd

# Demander à l'utilisateur d'entrer le chemin du fichier
file_path = input("Veuillez coller le chemin complet du fichier XLS : ")

# Charger le fichier XLS dans un DataFrame
data_original = pd.read_excel(file_path)

# Afficher le contenu du DataFrame
data_original

Installer les bibliothèques nécessaires

Copiez le code ci-dessous et collez-le sous Google Colab :

!pip install factor_analyzer
!pip install --upgrade scikit-learn
!pip install --upgrade --no-deps scikit-learn
!pip install --upgrade imbalanced-learn xgboost

Procéder à l’Analyse en Composantes Principales sans rotation

Copiez le code ci-dessous et collez-le sous Google Colab :

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from factor_analyzer import FactorAnalyzer
from factor_analyzer.factor_analyzer import calculate_kmo, calculate_bartlett_sphericity
from ipywidgets import interactive
import ipywidgets as widgets

# Fonction pour calculer l'alpha de Cronbach
def cronbach_alpha(df):
  if len(df.columns) > 1:
    k = df.shape[1]
    variances = df.var(axis=0, ddof=1)
    total_variance = df.sum(axis=1).var(ddof=1)
    return (k / (k - 1)) * (1 - (variances.sum() / total_variance))

  else:
    print("⚠️ Pas assez de variables pour calculer l'alpha sans item.")

# Chargement des données (supposées déjà chargées dans data_original)
def select_columns(data):
    print("\nColonnes disponibles :", list(data.columns))
    selected_columns = input("Entrez les noms des colonnes pour l'ACP (séparées par une virgule) : ").strip().split(',')
    selected_columns = [col.strip() for col in selected_columns]
    if not all(col in data.columns for col in selected_columns):
        print("Erreur : certaines colonnes n'existent pas. Réessayez.")
        return select_columns(data)
    return selected_columns

# Étape 1 : Sélection des colonnes pour l'ACP
selected_columns = select_columns(data_original)
df = data_original[selected_columns]

# Étape 2 : Normalisation des données
scaler = StandardScaler()
data_scaled = scaler.fit_transform(df)

# Étape 3 : Test KMO et Bartlett
kmo_all, kmo_model = calculate_kmo(df)
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print(f"\nKMO global : {kmo_model:.3f}")
print(f"Test de Bartlett : Chi² = {chi_square_value:.3f}, p = {p_value:.3f}")

# Étape 4 : Communalités
# Affichage des communalités
fa_temp = FactorAnalyzer(rotation=None, method='principal', is_corr_matrix=False)
fa_temp.fit(data_scaled)
eigenvalues, _ = fa_temp.get_eigenvalues()
n_factors = sum(eigenvalues > 1)
print(f"Nombre de composantes retenues (valeurs propres > 1) : {n_factors}")
fa_temp = FactorAnalyzer(rotation=None, method='principal', n_factors=n_factors,is_corr_matrix=False)
fa_temp.fit(data_scaled)
communalities = pd.DataFrame({
    'Variable': df.columns,
    'Initial': [1.000] * len(df.columns),  # Les valeurs initiales sont toujours 1
    'Communalité': fa_temp.get_communalities()
}).round(3)
print("\nCommunalités des variables:")
print(communalities)

# Étape 5 : Détermination du nombre de facteurs
eigenvalues, _ = fa_temp.get_eigenvalues()
n_factors = sum(eigenvalues > 1)
print(f"Nombre de composantes retenues (valeurs propres > 1) : {n_factors}")

# Tableau des variances expliquées
explained_variance_ratio = eigenvalues / np.sum(eigenvalues)
cumulative_variance = np.cumsum(explained_variance_ratio)
variance_table = pd.DataFrame({
    'Composante': [f"Composante {i+1}" for i in range(len(eigenvalues))],
    'Valeurs propres': eigenvalues,
    'Variance expliquée (%)': explained_variance_ratio * 100,
    'Variance expliquée cumulée (%)': cumulative_variance * 100
}).round(3)
display(variance_table)

# Graphique Scree Plot
plt.figure(figsize=(8, 6))
plt.plot(range(1, len(eigenvalues) + 1), eigenvalues, marker='o')
plt.title("Graphique des valeurs propres (Scree Plot)")
plt.xlabel("Composantes")
plt.ylabel("Valeurs propres")
plt.grid(True)
plt.show()

# Étape 6 : Choix du nombre de facteurs par l'utilisateur

# Demander à l'utilisateur le nombre de composantes à retenir au moment de la sauvegarde
n_factors = int(input("Entrez le nombre de composantes à retenir pour les scores factoriels : "))

# Étape 7 : Analyse factorielle avec le nombre de facteurs sélectionné
fa = FactorAnalyzer(rotation=None, method='principal', n_factors=n_factors)
fa.fit(data_scaled)

# Matrice des charges factorielles
loadings = fa.loadings_
components_matrix = pd.DataFrame(loadings, index=df.columns).round(3)
display(components_matrix)

# Étape 8 : Cercle des corrélations
if n_factors > 1:
    fig, ax = plt.subplots(figsize=(6, 6))
    ax.set_xlim(-1, 1)
    ax.set_ylim(-1, 1)
    ax.axhline(0, color='black', linestyle='-', linewidth=0.8)
    ax.axvline(0, color='black', linestyle='-', linewidth=0.8)
    ax.grid(True, linestyle='--', linewidth=0.5, alpha=0.7)
    for i in range(loadings.shape[0]):
        ax.scatter(loadings[i, 0], loadings[i, 1], color='b', alpha=0.5, s=50)
        ax.text(loadings[i, 0], loadings[i, 1], df.columns[i], color='r', fontsize=8, ha='center')
    ax.set_title("Cercle des corrélations", fontsize=10)
    ax.set_xlabel("Composante 1")
    ax.set_ylabel("Composante 2")
    plt.show()

# Demander à l'utilisateur s'il souhaite une rotation
rotation_choice = input("Souhaitez-vous procéder à une rotation des variables ? (oui/non) : ").strip().lower()

if rotation_choice == "non":
    fa = FactorAnalyzer(n_factors=n_factors, rotation=None, method='principal')
    fa.fit(data_scaled)
    factor_scores = fa.transform(data_scaled)
    # Demander à l'utilisateur le nom des composantes
    component_names = []
    for i in range(n_factors):
      name = input(f"Entrez le nom pour la composante {i+1} : ")
      component_names.append(name)
    components_matrix.columns = component_names


    factor_scores_df = pd.DataFrame(factor_scores, columns=component_names)

    # Affichage des scores factoriels
    display(factor_scores_df)


    # Calcul de l'alpha de cronbach
    global_alpha = cronbach_alpha(df)
    print(f"Alpha de Cronbach global : {global_alpha:.3f}")

    alpha_sans_item = {col: cronbach_alpha(df.drop(columns=[col])) for col in selected_columns}
    df_alpha = pd.DataFrame.from_dict(alpha_sans_item, orient='index', columns=['Alpha sans item']).round(3)
    display(df_alpha)


############# ROTATION ##################@@



else:
    rotation_types = ["varimax", "promax", "oblimin", "quartimax"]
    print("Types de rotation disponibles :", rotation_types)
    rotation_type = input("Veuillez entrer le type de rotation souhaité : ").strip().lower()

    if rotation_type not in rotation_types:
        print("Type de rotation non valide. Par défaut, 'varimax' sera utilisé.")
        rotation_type = "varimax"

    fa = FactorAnalyzer(n_factors=n_factors, rotation=rotation_type, method='principal')
    fa.fit(data_scaled)
    loadings = fa.loadings_
    components_matrix = pd.DataFrame(loadings, index=df.columns).round(3)


# Affichage des scores factoriels
#    display(factor_scores_df)

# Étape 8 : Cercle des corrélations
    if n_factors > 1:
        fig, ax = plt.subplots(figsize=(6, 6))
        ax.set_xlim(-1, 1)
        ax.set_ylim(-1, 1)
        ax.axhline(0, color='black', linestyle='-', linewidth=0.8)
        ax.axvline(0, color='black', linestyle='-', linewidth=0.8)
        ax.grid(True, linestyle='--', linewidth=0.5, alpha=0.7)
        for i in range(loadings.shape[0]):
            ax.scatter(loadings[i, 0], loadings[i, 1], color='b', alpha=0.5, s=50)
            ax.text(loadings[i, 0], loadings[i, 1], df.columns[i], color='r', fontsize=8, ha='center')
        ax.set_title("Cercle des corrélations", fontsize=10)
        ax.set_xlabel("Composante 1")
        ax.set_ylabel("Composante 2")
        plt.show()

# Demander à l'utilisateur le nom des composantes
    component_names = []
    for i in range(n_factors):
      name = input(f"Entrez le nom pour la composante {i+1} : ")
      component_names.append(name)
    components_matrix.columns = component_names
    factor_scores = fa.transform(data_scaled)
    factor_scores_df = pd.DataFrame(factor_scores, columns=component_names)

    # Affichage des scores factoriels
    display(factor_scores_df)
    global_alpha = cronbach_alpha(df)
    print(f"Alpha de Cronbach global : {global_alpha:.3f}")

    alpha_sans_item = {col: cronbach_alpha(df.drop(columns=[col])) for col in selected_columns}
    df_alpha = pd.DataFrame.from_dict(alpha_sans_item, orient='index', columns=['Alpha sans item']).round(3)
    display(df_alpha)

def generate_pca_summary(data_original, n_factors, fa, kmo_model, global_alpha, eigenvalues):
    """
    Génère un tableau de synthèse des résultats de l'ACP si une seule dimension est retenue.
    
    Args:
        df (pd.DataFrame): Les données utilisées pour l'ACP.
        n_factors (int): Nombre de facteurs extraits.
        fa (FactorAnalyzer): Analyseur factoriel après ajustement des données.
        kmo_model (float): Indice KMO global.
        alpha_cronbach (float): Alpha de Cronbach de l'échelle.
        eigenvalues (list): Valeurs propres des composantes.

    Returns:
        pd.DataFrame: Un tableau de synthèse des résultats.
    """
    if n_factors == 1:
        communalities = fa.get_communalities()
        loadings = fa.loadings_

        summary_data = []
        for i, var in enumerate(df.columns):
            summary_data.append([
                var,
                loadings[i][0],
                "-",  # Alpha sans item (à calculer si nécessaire)
                communalities[i],
                1.000 if i == 0 else round(np.corrcoef(df.iloc[:, 0], df.iloc[:, i])[0, 1], 3)
            ])

        summary_data.append(["KMO", kmo_model, "-", "-", "-"])
        summary_data.append(["α de l’échelle", global_alpha, "-", "-", "-"])
        summary_data.append(["Valeur propre du facteur", eigenvalues[0], "-", "-", "-"])
        summary_data.append(["Variance expliquée", round((eigenvalues[0] / sum(eigenvalues)) * 100, 3), "-", "-", "-"])


        columns = ["Items", "Contributions factorielles", "α sans item", "Qualité Extraction", "Correl. Items"]
        return pd.DataFrame(summary_data, columns=columns)
    
    return None  # Retourne None si plus d'un facteur est extrait

# Génération du tableau si une seule dimension est extraite
pca_summary = generate_pca_summary(data_original, n_factors, fa, kmo_model, global_alpha, eigenvalues)

# Affichage du tableau
if pca_summary is not None:
    #import ace_tools as tools
    #tools.display_dataframe_to_user(name="Tableau de Synthèse PCA", dataframe=pca_summary)
    #print(pca_summary)
    from IPython.display import display
    display(pca_summary)

# Demander à l'utilisateur s'il souhaite enregistrer les résultats
def save_results():
    global data_original
    data_original = pd.concat([data_original, factor_scores_df], axis=1)
    output_file = "Analyse_Factorielle_Resultats.xlsx"
    with pd.ExcelWriter(output_file) as writer:
        factor_scores_df.to_excel(writer, sheet_name="Scores_Factoriels", index=False)
        df_alpha.to_excel(writer, sheet_name="Alpha_Cronbach", index=True)
    print(f"\nLes résultats ont été sauvegardés dans {output_file}.")

save_btn = widgets.Button(description="Enregistrer les résultats")
save_btn.on_click(lambda b: save_results())
display(save_btn)

Un bout de code pour sauvegarder votre fichier contenant les scores factoriels des ACP réalisées

data_original.to_excel('data_original.xlsx', index=False)

# Télécharger le fichier Excel automatiquement sur votre ordinateur (spécifique à Google Colab)
from google.colab import files
files.download('data_original.xlsx')