1. Présentation des Résultats de la Régression Multiple
Dans cette section, les résultats obtenus par la régression multiple sont présentés de manière factuelle, sans interprétation. L’objectif est de fournir les indicateurs essentiels permettant d’évaluer la qualité du modèle et la pertinence des relations entre les variables.
La régression multiple est une méthode statistique permettant d’analyser l’influence de plusieurs variables indépendantes sur une variable dépendante. Elle fournit des résultats sous forme de coefficients et d’indicateurs statistiques qui permettent d’évaluer la robustesse du modèle.
2. Les Principaux Indicateurs à Présenter
2.1. Le Coefficient de Détermination (R² et R² Ajusté)
Le coefficient de détermination (R²) mesure la proportion de variance expliquée par le modèle de régression. Il indique dans quelle mesure les variables indépendantes permettent de prédire la variable dépendante.
- Une valeur de R² proche de 1 signifie que le modèle explique une grande part de la variance observée.
- Une valeur faible suggère que d’autres facteurs non inclus dans le modèle influencent la variable dépendante.
Le R² ajusté est une version corrigée du R² qui prend en compte le nombre de variables explicatives du modèle. Il est souvent préféré au R² brut car il pénalise l’ajout de variables non pertinentes et donne une estimation plus fiable de la qualité du modèle.
2.2. Les Coefficients de Régression
Les coefficients de régression indiquent l’impact de chaque variable indépendante sur la variable dépendante. Chaque coefficient est accompagné de sa signification statistique (p-value) qui permet de déterminer s’il est significatif ou non.
- Un coefficient positif signifie que la variable indépendante a un effet positif sur la variable dépendante.
- Un coefficient négatif indique un effet inverse.
- Une p-value inférieure à 0,05 suggère que la relation est statistiquement significative.
La présentation des coefficients sous forme de tableau permet d’identifier quelles variables ont un impact réel et lesquelles n’en ont pas.
2.3. Le Facteur d’Inflation de la Variance (VIF)
Le Variance Inflation Factor (VIF) est un indicateur permettant de détecter la multicolinéarité entre les variables indépendantes. Une forte corrélation entre ces variables peut fausser les résultats de la régression et compromettre l’interprétation des coefficients.
- Un VIF inférieur à 5 est généralement acceptable.
- Un VIF supérieur à 10 indique une forte multicolinéarité, ce qui peut nécessiter une révision du modèle.
2.4. La Significativité Globale du Modèle (Test de Fisher – F-statistic)
Le test de Fisher (F-statistic) permet d’évaluer si l’ensemble des variables indépendantes a un effet significatif sur la variable dépendante.
- Une p-value associée au test F inférieure à 0,05 indique que le modèle global est statistiquement significatif.
- Si la p-value est supérieure à ce seuil, cela signifie que les variables indépendantes n’expliquent pas significativement la variation de la variable dépendante.
3. Présentation Synthétique des Résultats
Un tableau récapitulatif des résultats doit être intégré dans le travail pour faciliter la compréhension.
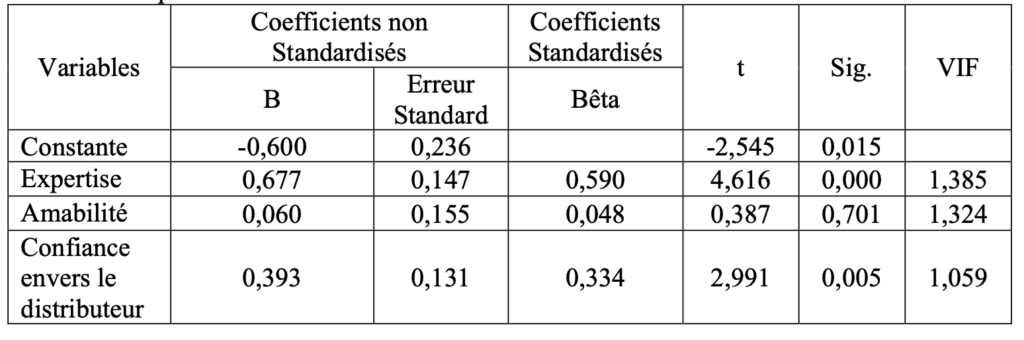
La présentation de ces résultats permet d’établir une base solide pour l’interprétation et la discussion qui suivra dans la section suivante.
- Une p-value associée au test F inférieure à 0,05 indique que le modèle global est statistiquement significatif.
- Si la p-value est supérieure à ce seuil, cela signifie que les variables indépendantes n’expliquent pas significativement la variation de la variable dépendante.
CODE PYTHON POUR RÉALISER LA RÉGRESSION MULTIPLE
Copiez le code ci-dessous et collez-le sous Google Colab :
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor
# Sélectionner les variables explicatives (X) et la variable dépendante (y)
y_var = input("Entrez le nom de la variable dépendante : ").strip()
X_vars = input("Entrez les noms des variables explicatives (séparés par une virgule) : ").strip().split(",")
# Vérification des variables
if y_var not in data_original.columns or any(var not in data_original.columns for var in X_vars):
raise ValueError("Erreur : Assurez-vous que toutes les variables existent dans le DataFrame.")
# Définir X et y
X = data_original[X_vars] # Suppression de l'ajout de la constante
y = data_original[y_var]
# Vérifier si X contient au moins une variable
if X.shape[1] == 0:
raise ValueError("Erreur : Aucune variable explicative valide sélectionnée.")
# Ajustement du modèle OLS
model = sm.OLS(y, X).fit()
print(model.summary())
# Vérification de la normalité des résidus avec un QQ-plot
residuals = model.resid
fig, ax = plt.subplots(figsize=(6, 6))
sm.qqplot(residuals, line="s", ax=ax)
ax.set_title("QQ-Plot des résidus")
plt.show()
# Vérification de l'hétéroscédasticité avec un scatter plot
plt.figure(figsize=(8, 5))
sns.scatterplot(x=model.fittedvalues, y=residuals)
plt.axhline(0, linestyle="dashed", color="red")
plt.xlabel("Valeurs ajustées")
plt.ylabel("Résidus")
plt.title("Graphique des résidus")
plt.show()
# Calcul du VIF pour détecter la multicolinéarité
if X.shape[1] > 1: # Vérifier que le VIF peut être calculé
vif_data = pd.DataFrame({
"Variable": X.columns,
"VIF": [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
})
print("\n📊 Facteur d'inflation de la variance (VIF) :")
display(vif_data)
# Interprétation du VIF
high_vif = vif_data[vif_data["VIF"] > 10]
if not high_vif.empty:
print("\n⚠️ Attention : Certaines variables présentent une forte multicolinéarité (VIF > 10). Cela peut affecter la fiabilité des coefficients estimés.")
print(high_vif)
else:
print("✅ Aucune multicolinéarité préoccupante détectée (VIF < 10).")
else:
print("\n⚠️ Pas assez de variables pour calculer le VIF.")
# Test de normalité des résidus (Jarque-Bera)
jb_stat, jb_pvalue, skew, kurtosis = sm.stats.jarque_bera(residuals)
print("\n📊 Résultats du Test de normalité de Jarque-Bera :")
print(f" - Statistique JB : {jb_stat:.3f}")
print(f" - p-value : {jb_pvalue:.5f}")
print(f" - Asymétrie (Skewness) : {skew:.3f}")
print(f" - Aplatissement (Kurtosis) : {kurtosis:.3f}")
# Interprétation automatique
test_result = "✅ Les résidus suivent une loi normale (p > 0.05)." if jb_pvalue > 0.05 else "❌ Les résidus ne suivent PAS une loi normale (p ≤ 0.05)."
print(f"\n{test_result}")
if jb_pvalue <= 0.05:
if abs(skew) > 1:
print("🔍 Problème détecté : **Asymétrie élevée** (skewness).")
print("✅ Solution : Essayez une transformation logarithmique ou une normalisation.")
if kurtosis < 2 or kurtosis > 4:
print("🔍 Problème détecté : **Aplatissement anormal (kurtosis).**")
print("✅ Solution : Vérifiez s'il y a des valeurs aberrantes (outliers).")
print("\n📌 Recommandations supplémentaires :")
print(" - Vérifiez la présence de valeurs aberrantes avec un boxplot.")
print(" - Testez une transformation (log, carré, racine) sur la variable dépendante.")
print(" - Ajoutez éventuellement d'autres variables explicatives.")
# Conclusion générale
print("\n📌 **Conclusion** :")
print(" - L'ajustement du modèle est évalué avec le R² et le R² ajusté.")
print(" - Un R² élevé (>0.7) indique une bonne capacité explicative du modèle, tandis qu'un R² faible suggère un ajustement limité.")
print(" - Les coefficients et leurs p-values indiquent la significativité des variables explicatives : une p-value < 0.05 signifie que la variable a un impact significatif.")
print(" - Le VIF aide à détecter la multicolinéarité, qui peut biaiser les estimations.")
print(" - Le test de Jarque-Bera vérifie la normalité des résidus, influençant la validité des tests de significativité.")