L’analyse en composantes principales (ACP) est une méthode statistique qui permet de réduire la dimensionnalité d’un ensemble de données. Elle est couramment utilisée en marketing pour regrouper des items d’une échelle de mesure en dimensions ou facteurs cohérents.
Dans le cadre du développement d’une échelle de mesure, l’ACP est utilisée pour déterminer la structure sous-jacente des items de l’échelle. L’objectif est de regrouper les items en dimensions qui sont cohérentes avec le concept à mesurer.
La construction de l’ACP se déroule en quatre étapes :
Etape 1 – Collecte des données
Les données sont collectées auprès d’un échantillon de participants, à l’aide d’une échelle de mesure composée d’un ensemble d’items. Les données collectées sont généralement des scores sur une échelle de Likert à cinq points, allant de “tout à fait en désaccord” à “tout à fait d’accord”.
Etape 2 – Calcul de la matrice de covariance
La matrice de covariance est une matrice qui mesure la covariance entre les items de l’échelle. La covariance est une mesure de la dépendance entre deux variables.
Etape 3 – Calcul des valeurs propres et des vecteurs propres
Les valeurs propres mesurent l’importance des facteurs, tandis que les vecteurs propres indiquent comment les items sont associés à chaque facteur.
Les valeurs propres sont calculées en utilisant la matrice de covariance. La valeur propre la plus élevée correspond au facteur le plus important, et ainsi de suite.
Les vecteurs propres sont calculés en diagonalisant la matrice de covariance. La diagonalisation est une opération mathématique qui permet de transformer une matrice en une matrice diagonale, dont les éléments de la diagonale sont les valeurs propres.
Etape 4 – Sélection des facteurs
Les facteurs sont sélectionnés en fonction de leur importance et de leur cohérence avec le concept à mesurer.
L’importance d’un facteur est déterminée par sa valeur propre. Un facteur est considéré comme important si sa valeur propre est supérieure à une certaine valeur seuil, qui est généralement fixée à 1.
La cohérence d’un facteur est déterminée par la façon dont les items sont associés à ce facteur. Un facteur est considéré comme cohérent si les items qui lui sont associés sont corrélés entre eux.
L’interprétation des facteurs est une étape importante de l’ACP. Elle consiste à attribuer un nom à chaque facteur et à définir ce qu’il mesure.
L’interprétation des facteurs peut être réalisée en se basant sur la définition du concept à mesurer, ainsi que sur les items qui sont associés à chaque facteur.
Exemple : Test d’une échelle de mesure de l’attitude à l’égard du shopping
Dans le cadre d’une étude consacrée au Shopping, la revue de littérature fait apparaître que l’attitude des consommateurs à l’égard du shopping peut être mesure en utilisant 2 dimensions : le plaisir et l’économie.
Les items correspondant à chacune de ces dimensions sont les suivants :
- Plaisir :
- Le shopping est amusant (V1)
- Je profite du shopping pour manger à l’extérieur (V3)
- Le shopping ne m’intéresse pas (V5)
- Economie :
- Le shopping est mauvais pour le budget (V2)
- J’essaie de trouver les meilleures affaires quand je fais du shopping (V4)
- Je peux économiser beaucoup d’argent en comparant les prix (V6)
Dans le cadre d’un pré-test, une étude quantitative a été réalisée sur un échantillon de 20 personnes où les consommateurs ont exprimé leur degré d’accord avec chaque item sur une échelle en 7 points (1 = n’est pas du tout d’accord – 7 = est d’accord) :
V1 = le shopping est amusant
V2 = le shopping est mauvais pour le budget
V3 = je profite du shopping pour manger à l’extérieur
V4 = j’essaie de trouver les meilleures affaires quand je fais du shopping
V5 = le shopping ne m’intéresse pas
V6 = vous pouvez économiser beaucoup d’argent en comparant les prix
Une analyse en composantes principales est réalisée avec les données recueillies afin de vérifier la structure factorielle de l’échelle.
Résultats
Le premier tableau présente une synthèse des statistiques descriptives, moyenne et écart-type pour chacune des variables observées.

On observe ensuite la matrice des corrélations ainsi que les coefficients de signification. Une corrélation mesure l’intensité d’une relation entre deux variables. Une corrélation peut prendre une valeur située entre -1 et 1. Une valeur proche de 1 indique que les variables sont fortement liées et évoluent dans le même sens. Une corrélation de 0 indique une absence de lien.
Si plusieurs variables sont corrélées (corrélation > 0.5 et surtout Signification < 0,05), la factorisation est possible. Si non, la factorisation n’a pas de sens et n’est donc pas conseillée.

La matrice des corrélations est diagonale. Cela veut dire que vous disposez de tous les liens en lisant la partie du basse du tableau des corrélations.
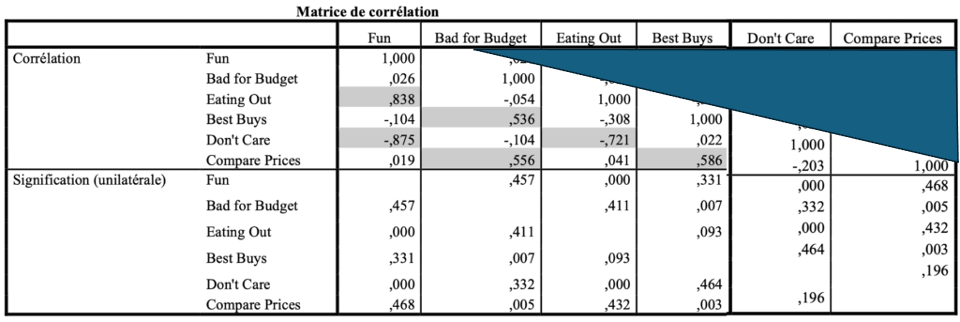
Dans notre exemple, plusieurs variables sont correllées entre elles :
- V1, V3 et -V5
- V2, V4 et V6
Dans un deuxième temps, il faut observer l’indice de KMO (Kaiser-Meyer-Olkin) qui doit tendre vers 1. si ce n’est pas le cas, la factorisation n’est pas conseillée. Pour juger de l’indice de KMO, on peut utiliser l’échelle suivante :
- 0,50 et moins est misérable
- entre 0,60 et 0,70, c’est médiocre
- entre 0,70 et 0,80 c’est moyen
- entre 0,80 et 0,90 c’est méritoire
- et plus 0,9 c’est merveilleux.
Enfin, on utilise le test de sphéricité de Bartlett. : si la signification (Sig.) tend vers 0.000, c’est très significatif, inférieur à 0.05 significatif, entre 0.05 et 0.10 acceptable et au dessus de 0.10, on rejette.

Si l’ACP satisfait à au moins deux de ces trois conditions, on peut continuer. C’est le cas pour notre analyse. Pour choisir les variables à éliminer, on observe leur qualité de représentation : plus la valeur associée à la ligne « Extraction » est faible, moins la variable explique la variance.

Combien d’axes retenir
Trois règles sont applicables :
- 1ere règle : la règle de Kaiser qui veut qu’on ne retienne que les facteurs aux valeurs propres supérieures à 1.
- 2eme règle : on choisit le nombre d’axe en fonction de la restitution minimale d’information que l’on souhaite. Par exemple, on veut que le modèle restitue au moins 80% de l’information. Pour ces deux premières règles, on examine le tableau « Variance Totale Expliquée ». Dans notre cas, 2 composantes (axes) ont une valeur propre supérieure à 1 pour une variance totale expliquée de 80,238%.

3eme méthode : le « Scree-test » ou test du coude. On observe le graphique des valeurs propres et on ne retient que les valeurs qui se trouvent à gauche du point d’inflexion. Graphiquement, on part des composants qui apportent le moins d’information (qui se trouvent à droite), on relie par une droite les points presque alignés et on ne retient que les axes qui sont au dessus de cette ligne.
Ici, le point d’inflexion est entre les composantes 2 et 3. On retient donc 2 axes.

Interprétation des résultats
Ici, l’objectif consiste à donner un sens à un axe grâce à une recherche lexicale (ou recherche de mots) à partir des coordonnées des variables et des individus. Ce sont les éléments extrêmes qui concourent à l’élaboration des axes.

Dans notre exemple :
• Les variables « Fun » et « Eating Out » sont celles qui concourent le plus à la formation de l’axe 1 pour sa portion positive et la variable « Don’t care » pour sa partie négative.
• Les variables « Best Buys », « Bad for Budget » et « Compare Prices » contribuent à la formation de l’axe 2.
Le diagramme des composantes donne une représentation graphique des axes et des variables qui contribuent à leurs formations.

La partie positive de l’axe 1 représente l’intérêt pour le shopping.
La partie négative de l’axe 1 représente le désintérêt à l’égard du shopping.
La partie positive de l’axe 2 représente l’intérêt pour les affaires dans le cadre du shopping.

La matrice des co-variances indique que les deux composantes sont orthogonales.

L’ACP fournit aussi les coordonnées de chaque individu sur les deux axes retenus, FAC1_1 pour l’axe X et FAC1_2 pour l’axe Y.
Références
Churchill, G. A. Jr. (1979). A paradigm for developing better measures of marketing constructs. Journal of Marketing Research, 16(1), 64-73.
Hair, J. F., Black, W. C., Babin, B. J., Anderson, R. E., & Tatham, R. L. (2010). Multivariate data analysis (7th ed.). Upper Saddle River, NJ: Pearson Education.
Malhotra, N. K. (2017). Marketing research: An applied orientation (8th ed.). Harlow, England: Pearson Education.